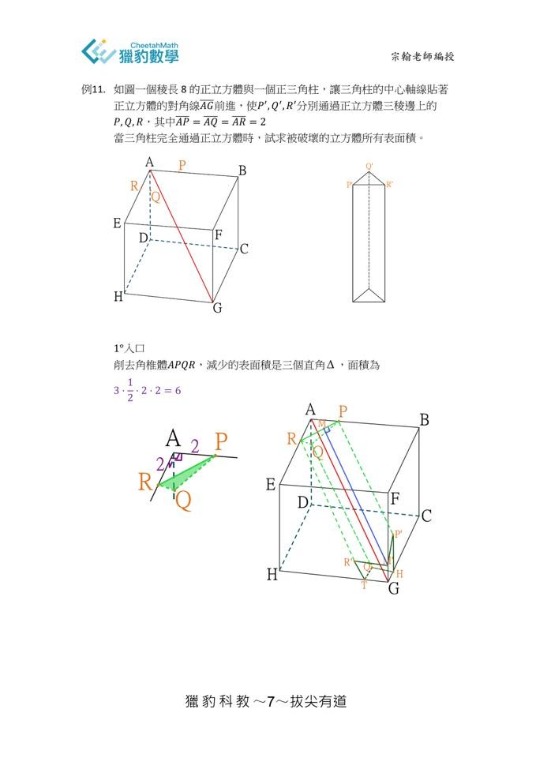
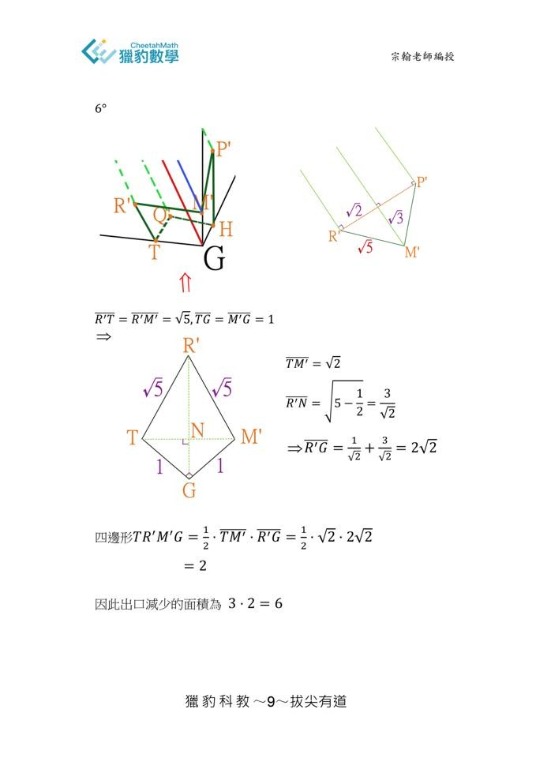
獵豹有獎問徵答解答(宗翰提供)
1. 引理:
首先複習一個屬於高中課綱的重要知識:
兩個平面E,F的銳交角為θ,
平面E上一個封閉區域A,面積為S
區域A對平面F的正投影區域B
=> 其面積為S·COSθ
2.先討論一對平行軸面:
(正三角形PQR)與(正三角形P’Q’R’)全等,且兩平面平行。
很明顯
(三角形PAQ)投影在(PQR平面)的面積
=(四邊形TR’M’G)投影在(P’Q’R’平面)的面積
皆為
(正三角形)面積的1/3 ;
(ABCD平面)//(EFGH平面)
故
「(ABCD平面)與(PQR平面)的夾角
=(EFGH平面)與(P’Q’R’平面)的夾角」
易由引理知
(三角形PAQ)與(四邊形TR’M’G)的面積相等:皆為2
3.由於三個軸面的對稱性,便得出結論。
https://www.facebook.com/groups/695697124716309/permalink/985861825699836/